支持向量机(SVM)是90年代中期发展起来的基于统计学习理论的一种机器学习方法,通过寻求结构化风险最小来提高学习机泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本量较少的情况下,亦能获得良好统计规律的目的。
通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,即支持向量机的学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。

至于核技巧的理解如图:
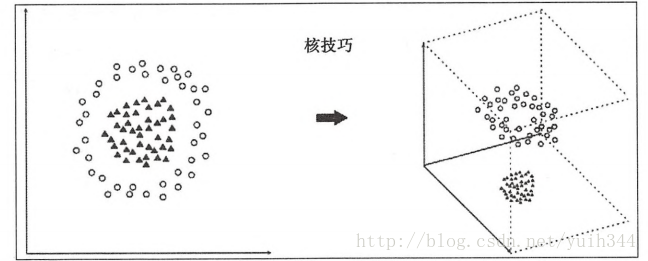
核技巧将线性不可分的模型映射到高维空间,变得线性可分,通过核函数的映射三维空间可以通过二维平面进行划分,一般来说映射到高维空间后计算复杂度会增加,其消耗的时间也会增加。
对于线性可分的问题,SVM是等价与感知器的,详见http://yangtian.xyz/machine-learning-Sensor 只不过
在此基础上保持几何间隔最大化,几何间隔最大的超平面是唯一的,几何间隔最大可以理解为在一定程度上保持距离超平面最近的点也有一定的确信度将其分开,也可以理解为一定程度上避免过拟合,拥有很好的预测能力。

于是求解几何间隔最大问题可以转化为

以上等式可以通过对偶算法来求解,至于对偶算法,详见https://www.zhihu.com/question/26658861/answer/53394624 知乎上作者的回答比较详尽,求解对偶算法时应用到了拉格朗日算子
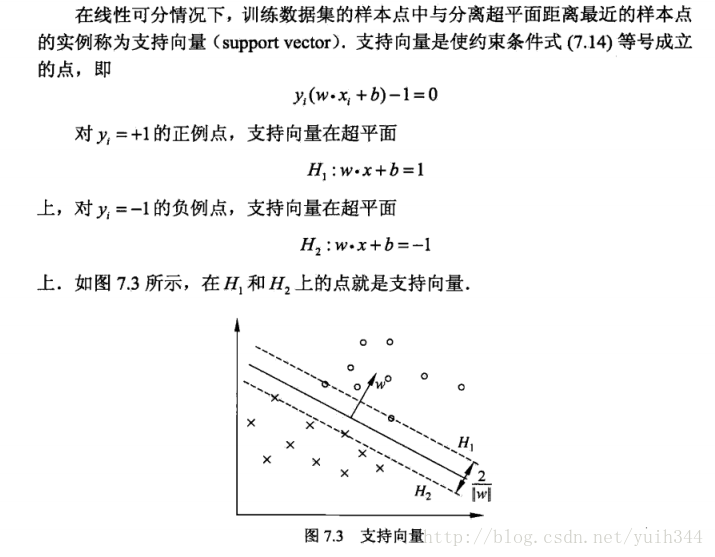
 引入支持向量
引入支持向量
合页损失函数

非线性支持向量机与核函数

通过核函数将,欧式空间映射为特征空间(希尔伯特空间),来求解为线性可分问题
SMO算法求解凸二次优化问题的最优解

基本概念和理解的公式也就这么多,不得不说吐槽一下这节好多看不懂的数学推导,有机会的话回来补充,最后总结一下SVM的处境吧,16年据说是人工智能元年,李世石和AlphaGo大战体现了神经网络深度学习取得的进步,在此之前工业界SVM应用的是更加广泛的,但是呢神经网络就像一个黑盒一样,隐藏层的不同实现看似可以求解诸多以往无法解决的问题,也与SVM一样都可以解决线性不可分的问题,只不过实现不同,而SVM的数学性似乎更强一些有着严格的理论支撑也会收到一部分人的欢迎,至于现在很火热的深度学习神经网络和传统机器学习算法之间未来和前景,我这种渣渣还是不予置评,还是在学习中默默吃瓜,看看未来究竟还会带来怎样的改变呢,哈哈,拭目以待。
参考:《统计学习方法》-李航