为什么要用logistic回归?
我们在线性回归分析时,有时会遇到因变量y不是连续值,而是离散的,很多情况是0-1变量。如分析顾客对于商品行为的导致的结果是买(1)还是不买(0),分析股票的各种数据,因变量也是买(1)、不买(0)…。这种因变量如果我们还是使用线性回归,得到的直线一定与样本拟合得不好。举个例子,我们考察选民年收入和给某个候选人投票的相关性,如果我用线性回归来做。设回归方程为y=mx+b+e(为了严谨e为方程的干扰值,与x无关,服从正态分布,平均值为0)。显然,y=0,表示未投票;y=1表示投票。一定要记住由于e的存在,yi的值只能是一个统计值,也许每次的yi都不一样(夸张了点)。。因此因变量为二分类的线性规划模型又叫线性概率模型(linear probability model)。如果模型是线性的,很显然,如果xi是一个很大的值(如年收入1亿),那么我们得到的yi很可能大于1,相反如果年收入是一个很小的值(如-100000),那yi的值很可能得到一个小于0的值。实际上,这很可能是个分段函数模型,这对于线性回归就不方便计算了。
Logistic回归模型介绍
LR回归,虽然这个算法从名字上来看,是回归算法,但其实际上是一个分类算法,学术界也叫它logit regression, maximum-entropy classification (MaxEnt)或者是the log-linear classifier。在机器学习算法中,有几十种分类器,LR回归是其中最常用的一个。
LR回归是在线性回归模型的基础上,使用sigmoid函数,将线性模型 wTx 的结果压缩到[0,1] 之间,使其拥有概率意义。 其本质仍然是一个线性模型,实现相对简单。在广告计算和推荐系统中使用频率极高,是CTR预估模型的基本算法。同时,LR模型也是深度学习的基本组成单元。
LR回归属于概率性判别式模型,之所谓是概率性模型,是因为LR模型是有概率意义的;之所以是判别式模型,是因为LR回归并没有对数据的分布进行建模,也就是说,LR模型并不知道数据的具体分布,而是直接将判别函数,或者说是分类超平面求解了出来。
定义:
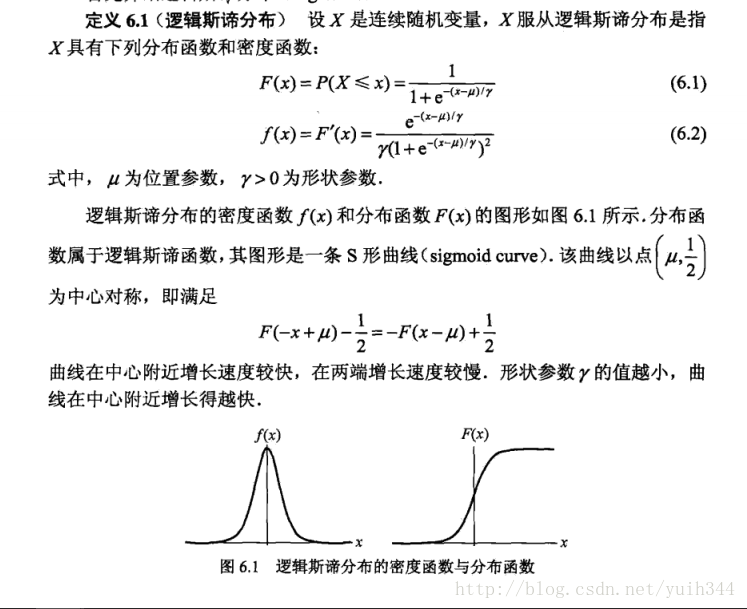
logistic回归模型:

模型参数估计:

扩展:
SVM和logistic回归分别在什么情况下使用?
两种方法都是常见的分类算法,从目标函数来看,区别在于逻辑回归采用的是logistical loss,svm采用的是hinge loss。这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。两者的根本目的都是一样的。此外,根据需要,两个方法都可以增加不同的正则化项,如l1,l2等等。所以在很多实验中,两种算法的结果是很接近的。
但是逻辑回归相对来说模型更简单,好理解,实现起来,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些。但是SVM的理论基础更加牢固,有一套结构化风险最小化的理论基础,虽然一般使用的人不太会去关注。还有很重要的一点,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算量。
参考:http://lib.csdn.net/article/machinelearning/34214
参考:统计学习方法-李航
参考:https://www.zhihu.com/question/21704547/answer/20293255– 来源知乎 作者orangeprince