前言:刚看的时候感觉这两个内容差不多,最小二乘法是沙老师讲智能与智能信息处理时候涉及的内容,梯度下降是来自于李宏毅老师的机器学习课程,仔细研究之后发现差别还是蛮大的。
最小二乘法
一开始对最小二乘法有所误解,广义的最小二乘法是一种目标,它通过最小化误差的平方和寻找数据的最佳函数匹配,并使得这些求得的数据与实际数据之间误差的平方和为最小,最小二乘法还可用于曲线拟合,因此,可以分为线性和非线性的最小二乘法。其中,线性最小二乘法具有闭式解,最终结果为全局最优,而非线性最小二乘法通常采用迭代法求解。
而狭义的最小二乘法指的是在线性回归下采用最小二乘准则(或者说叫做最小平方),进行线性拟合参数求解的、矩阵形式的公式方法。线性最小二乘法如图:
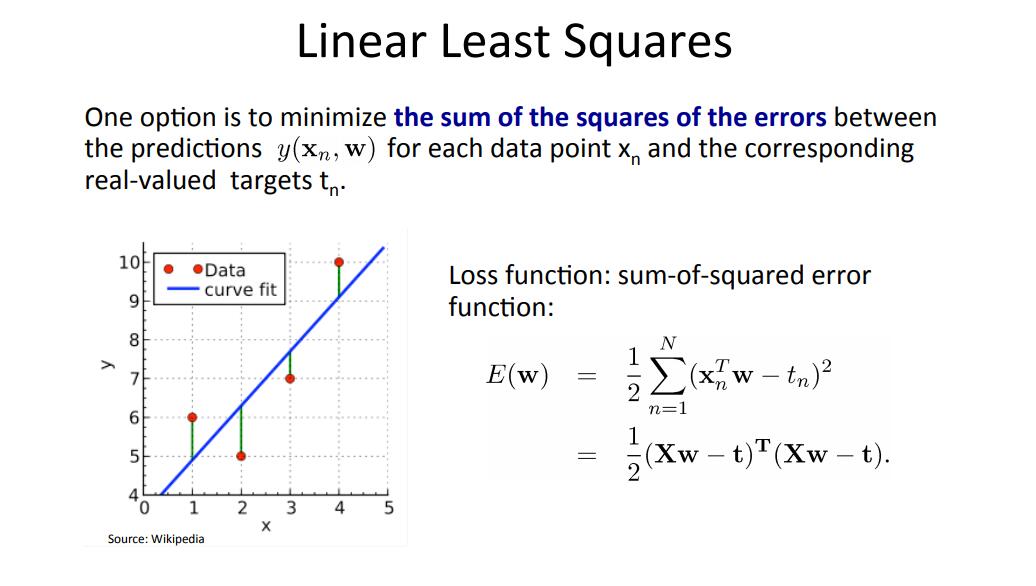
因此在线性回归的前提下,我们的目标是最小化loss function,采用最小二乘法思想就是把目标函数划归为矩阵运算问题,然后求导后等于0,从而得到极值。最终可以解得如下图的唯一解。

梯度下降优化(Adagrad 算法)
简单区分一下梯度下降和最小二乘法,来自于百度百科的解释是梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。因此说面梯度下降只是数值求解的具体操作,和最小二乘准则下面的最优化问题都可以用随机梯度下降求解。
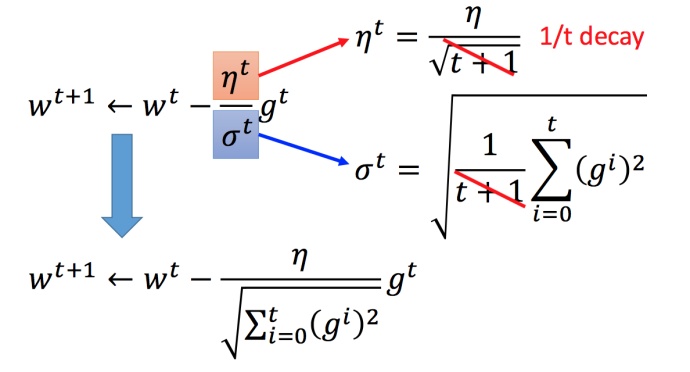
在梯度下降法中learning rate的大小并不好调整,因此我们可以采用自适应的learning rate,由此引出Adagrad 算法。
Adagrad 算法举例
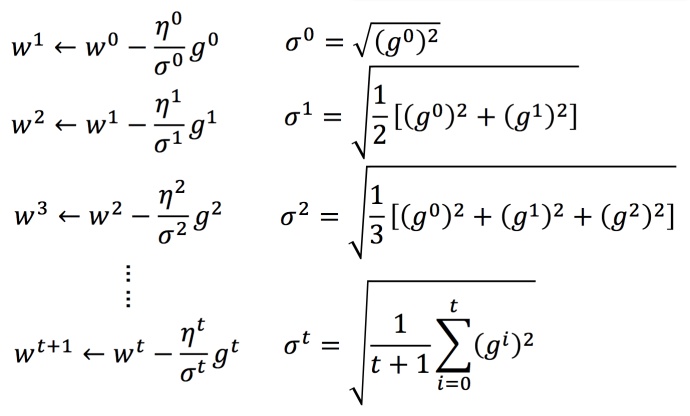
其中gt=∂L(θt)/∂w
w是一个参数,不是一组
σt:参数的所有微分的均方根,对于每个参数都是不一样的。
化简可得: